Conversion thermique électrique : demande de conseils
-
 Bonjour,
Bonjour,
On m'a donné un Piper J3 Cub en bois, aspect maquette, équipé servos fonctionnels, dont voici les principales caractéristiques :
envergure environ 1,70 m
longueur environ 1,25 m
poids environ 2,5 kg
moteur thermique "MDS 40" (sur internet, on trouve qu'il s'agirait d'un 6,5 cm3 pour environ 375 grammes).
J'ignore si cet avion a volé. Il est vieillot, mais en bon état.
Je souhaiterais le faire voler, ce qui nécessitera sans doute de remplacer les servos et d'y installer un récepteur moderne 2,4 GHz, mais je souhaiterais surtout le convertir à l'électrique. N'ayant jamais procédé à ce genre d'opération, je suis à la recherche de conseils dans un premier temps, d'aide dans un second temps si la conversion est possible.
Cette conversion vous semble-t-elle envisageable ? Quelles seraient les caractéristiques d'un moteur + hélice à installer sur un appareil pareil ? Cela m'aiderait aussi à avoir une première idée de budget ...
Mille merci pour vos retours. Au plaisir de se croiser au terrain.
Jean-Philippe -
Bonjour,
Je te joints ici un document qui te permettra de fail tous les calculs Ce document a été fait pour un piper de 2,3m. Mais il suffit de reprendre les calculs avec les bonnes spécifications
si tu as un mail je te fais parvenir le document..
le mien : daniel.selecki@laposte.net
Notes de Calcul du Piper Cup de 2,310 m envergure
1 / 21 27/11/2020
2 / 21
27/11/2020
Envergure (mm) : 2310 Longueur (mm) : 1 500 Poids (g) : 5 300 ~ 5 400 Surface (dm2) : 76
Constructeur
Piper Aircraft
Type
Avion léger à aile haute d'entraînement, de liaison et de reconnaissance
Premier vol
1938
Date de retrait
1947
Motorisation
Moteur
Continental A-65 de 65 ch
553 kg
Dimensions
Envergure
10,76 m
Longueur
6,83 m
Hauteur
2,042 m
Surface alaire
16,60 m2
Nombre de places
2 en tandem
Réservoirs
1 réservoir de 45 litres
Masses
Masse à vide
Environ 300 kg
Masse maximum
Performances
Décollage
245 m
Atterrissage
200 m
Vitesse de croisière
117 km/h
Vitesse maximale (VNE)
135 km/h
Vitesse de décrochage
63 km/h
Plafond
Théorique : 3 825 m Pratique : 3 155 m
Vitesse ascensionnelle
Au niveau de la mer : 2,8 m/s m/s
Distance franchissable
280 km
3 / 21 27/11/2020
1) 2) 3)
4) 5)
6) 7) 8) 9) 10) 11) 12) 13)
14)
SOMMAIRE
Profil d’aile
Vol de croisière à la finesse maximum
Cz, Cx de l’avion complet
3-1 Cz réel
3-2) Traînéeinduite
3-3) Traînéedufuselage
3-4) Traînée totale et finesse de l’avion complet
Vitesse minimum de vol (sans du flux d’air d’hélice) Vitesse de vol de croisière
Traînée à combattre à la vitesse de croisière Motorisation et batterie de propulsion
L’hélice
L’hélice au décollage
L’hélice en vol
Equation du moteur (Régime max)
Conséquences sur la distance et vitesse de décollage
Performance en Vol de croisière
13 1) Point de fonctionnement en J de l’hélice en croisière 13-2) Vitesse hélice en vol de croisière
13-3) Puissance en vol de croisière
13-4) Calcul du courant nécessaire en vol de croisière 13-5) Réglage du PWM en vol de croisière
Calcul de l’autonomie de vol
4 / 21
27/11/2020
1) Profil des ailes.
Le profil de l’aile du Piper Cup J3 est assimilé à un profil Clark Y.
Compte tenu d’une vitesse de vol minimum de l’ordre de 10 m/s ( 36 km/h) et d’une corde d’aile de 0,29m, le nombre de Reynolds à prendre en considération est voisin de :
Re = 10 *0,29 / (0,0000145) = 200 000
D’après cette estimation, la polaire de l’aile est celle tracée en vert.
Il apparaît que le Cz maximum est de 1,5. Ce paramètre permettra d’évaluer la vitesse minimum de vol et la vitesse de décollage compte tenu du poids estimé de l’avion.
Le Cx au décollage du profil est de 0,03 Le Cz max = 1,5
5 / 21 27/11/2020
2) Vol de croisière à la finesse maximum
La tangente à la polaire tracée depuis l’origine des axes Cz Cx permet de déterminer le point de finesse maximum du profil
Cz = 0,8 , Cx = 0,01, La finesse du profil est donc 80.
Remarque : Il ne faut pas associer les Cz et Cx du profil au Cx et Cz de l’avion complet, il y a lieu de corriger ces valeurs par les effets de bords dues à l’allongement de l’aile et au Cx du fuseau et empennage arrière.
3) Cz, Cx de l’avion complet
3-1) Czréel
L’allongement de l’aile principale du Piper Cup est le rapport entre l’envergure et la corde moyenne de l’aile
Ici l’envergure est de 2,310 m et la corde de 0,29m. L’allongement est donc A = 2 ,310 / 0,29 A = 7,97
Compte tenu de cet allongement, le coefficient de correction du Cz de la polaire pour obtenir le Cz de l’aile du Piper est C = A/( A+1,8)
C = 7,97 / ( 7,97 + 1,8 ) = 0,816
Ainsi le Cz max au décollage sera Cz polaire x coefficient correctif Cz max décollage = 1,5 x 0,816 = 1,224
De même le
Cz à la finesse maximum = 0,8 x0,816 = 0,653 3-2) Traînéeinduite
Les tourbillons en bout d’aile crée de la traînée induite qui modifie le Cx du profil
La traînée induite est donnée par le rapport Cz2/ (Π A )
Ainsi la traînée induite au décollage est Cz induit = 0,032 / ( 3,14 x 7,97 ) = 0,09 De même la traînée induite à la finesse maximum est 0,012 / ( 3,14 x 7,97 ) = 0,026
Aux trainées induites par les effets de bouts d’ailes, il faut ajouter la traînée du fuselage dont le maître couple est de 0,240 x 0,150 = 0,034 m2
6 / 21 27/11/2020
3-3) Traînéedufuselage
Le coefficient de traînée du fuselage est estimé à 0,2
Compte tenu que la surface du maître couple du fuselage est 0,240 x 0,140 = 0,034m2
Ainsi le coefficient de traînée du fuselage est 0,034 x 0,2 = 0,0064
Pour estimer la finesse globale de l’avion il faut ramener cette traînée du fuselage à la surface alaire, pour corriger les traînées de profil, et induite.
Le coefficient de traînée ramené à la surface alaire pour le fuselage est de 0,01
3-4) Traînéetotaleetfinessedel’avioncomplet
Ainsi le Cx global de l’avion en vol de croisière est
Cx avion = Cx polaire + Cx induit + Cx fuselage
Cx avion = 0,01 + 0,026 + 0,01 = 0,046
Ainsi la finesse réelle de l’avion est le rapport entre le Cz réel et le Cx avion La finesse du Piper est évaluée à 0,653 /0,046 = 14,2
4) Vitesse minimum de vol (sans tenir compte du flux d’air
d’hélice)
La vitesse minimum de vol est obtenue quand la portance générée par la vitesse est égale au poids de l’avion.
La portance est donnée par P = 1⁄2 d Cz S V2
Ou d est la densité de l’air ou l’avion vole. Celle-ci est prise à 1,2 kg /m3 S est la surface alaire de l’avion S = 0,67 m2
Le Cz est le Cz réel max de l’avion = 1,22
Le poids de l’avion est estimé à 5,320 kg
Ainsi l’équation donne une vitesse minimum de vol de V2 = 2 m g / ( d Cz S )
V2 = 2 x 5,32 x 9,81 / (1,2 x 1,22 x 0,67 ) = 106 m2/s2 V = 10,3 m/s ou 37 km/h
7 / 21
27/11/2020
5) Vitesse de vol de croisière
De même lorsque l’avion vole en configuration de finesse maximum. Le Cz à considérer est de 0,653
V2 = 2 x 5,32 x 9,81 / (0,653 x 1,22 x 0,67 ) = 195,5
V = 14 m/s ou V = 50 km/h
6) Traînée à combattre à la vitesse de croisière
Cette traînée ce calcule en considérant le Cx de l’avion complet et en adoptant la vitesse de vol de 14 m/s ou 50 km/h . Valeur du Cx = 0,046
T = 1⁄2 d Cx S V2
T = 1⁄2 1,2 x 0,046 x 0,67 x 195,5 = 3,61 N
La résistance de l’air est de 3,61 N ou environ de 0,367 kg
En fait cette traînée doit être compensée par la traction de l’hélice pour assurer cette vitesse de vol
7) Motorisation et batterie de propulsion
Sans chercher à optimiser les paramètres de propulsion, il est choisi une batterie LI-Po de 5Ah en 6 éléments ( soit dite 6S )
Le moteur électrique choisi est le Moteur Brushless Epower EP 4130-400 dont les principales caractéristiques sont données ci –après :
Kv = 385 Tm /V
Courant max = 60A (limité à 60 s )
Courant de fonctionnement de 18 A à 40 A Résistance interne = 54 mΩ
Rendement estimé à 0,88
Masse = 406 g
8 / 21
27/11/2020
La résistance interne de la batterie de propulsion est estimée à 12 mΩ ( 2 mΩ par élément )
8) L’hélice
Le choix de l’hélice va aussi conditionner les performances de l’avion.
Compte tenu que l’avion est sensible au vent notamment au décollage, il est recherché une traction importante dans cette phase de vol. Par ailleurs, la dimension maximum de l’hélice est limitée aussi par le courant maximum supporté par le moteur.
Dans le calcul qui suit, on adopte une hélice de 18 X 7,5 ( dimensions en pouces ), qui semble être proche de l’optimum. ( calage de l’hélice 10° )
L’utilisation d’une hélice avec un calage différent conduit à modifier les coefficients aérodynamiques de l’hélice Cp et Ct
9 / 21 27/11/2020
Ci-dessous le paramètre Ct pour différent calage d’hélice
10°
Ci-dessous les courbes d’hélice pour la détermination du Cp en fonction du calage
10 / 21 27/11/2020
La puissance à fournir à l’hélice est
P=CpdN^3 D^5
La traction développée par l’hélice en Newton est
T=Ct dN^2 D^4
9) L’hélice au décollage
On admettra que dans la phase de décollage, la vitesse de l’avion reste faible. Pour faciliter les calculs, les paramètres de l’hélice sont choisis à la vitesse 0. C'est-à-dire J = V/( ND ) = 0
V est la vitesse en m/s
D le diamètre de l’hélice en mètre
N la vitesse de rotation de l’hélice en tours /seconde
Ci dessous les paramètres de l’hélice pour J= 0 ( ou en point fixe )
Cp° = 0,021
Ct° = 0,083
Dans le principe du calcul qui sera détaillé plus loin, la puissance motrice développée par le moteur doit être absorbée par l’hélice. La puissance motrice absorbée par l’hélice est donnée par la formule
P = Cp d N^3 D^5
Il faut déterminer la formule donnant la puissance fournie par le moteur et égaler les 2 puissances
10) L’hélice en vol
Les paramètres de l’hélice vont évoluer avec le paramètre J = V /( ND).
Pour connaître le point de fonctionnement de l’hélice en vol il faudra tenir compte des données aérodynamiques de l’avion et des caractéristiques du moteur de propulsion associé à ces annexes (batterie, contrôleur)
11) Equation du moteur (Régime max)
Ci-dessous, le schéma d’alimentation du moteur de propulsion.
E représente la tension d’alimentation de la batterie dont la résistance interne est Rb
L’interrupteur et la résistance Rc représente le contrôleur assurant une modulation du courant selon un PWM.
Rm est la résistance interne du moteur I° est le courant à vide du moteur
11 / 21 27/11/2020
Si le courant total débité par la batterie est I = Im + I°
La tension aux bornes des enroulements supposés sans résistance est E – ( Rb + Rc + Rm ) I = Vm
Si R est la résistance totale du circuit
R = 12 + 2 + 54 = 68 mΩ
Vm = E – R ( I )
I= (E –Vm)/R
La vitesse de rotation du moteur est donnée par Tm = Kv Vm ou N = Kv Vm /60
La puissance disponible sur l’arbre est Pm = Vm Im ou en fonction du courant I débité par la batterie
Pm= Vm(I–I°)
I
Rb
E
RcRm Im
I°
Vm Kv
Comme la puissance absorbée par l’hélice est Pm = Cp d N^3 D^5 On a la relation Vm ( I – I° ) = Cp d N^3 D^5
Comme N = Kv Vm/60
Vm ( I – I° ) = Cp d [ Kv Vm /60 ]^3 D^5
En simplifiant par Vm
I – I° = Cp d Vm^2 Kv^3 D^5/ (60)^3 (A)
12 / 21
27/11/2020
La loi d’Ohm donne pour Vm = E – RI
Vm2 = E2 - 2 RI + R2 I2
La relation ( A ) ci-dessus s’écrit
I – I° = Cp d ( E2 - RI + R2 I2 ) Kv^3 D^5 / ( 60 )^3 Appellons Q = Cp d Kv^3 D^5 / ( 60)^3
Alors la relation s’écrit
I – I° = Q E2 - Q R I + Q R2 I2 ce qui se met sous la forme d’une équation du 2° degrés en I Q R2 I2 - [ QR + 1 ] I + Q E2 + I° = 0 avec Q = Cp d Kv^3 D^5 / ( 60)^3
Cette équation permet de trouver le courant I pour l’hélice donnée et pour le Kv spécifié.
Remarque
En fait, la présence du courant dans le moteur a tendance à faire baisser le Kv. Ainsi le Kv réel est donné par le Kv° du constructeur diminué par W Im ou W est un coefficient et I le courant moteur
Donc Kv = Kv° - W Im
La réduction du Kv est normalement de 10% au courant maximum Si Kv = 385
Le Kv à 60 A serait 385 – 38 = 347
Donc W = 38 /60 = 0,63
Le Kv à prendre en considération est
Kv = Kv° - 0,63 Im
Le calcul de façon manuel consiste à calculer I, puis Im = I – I° et de déterminer le Kv réel du moteur avec Kv = Kv° - 0,63 Im, ensuite réinjecter cette valeur de Kv dans l’équation du 2° degrés.
Il faut réitérer l’opération jusqu'à stabilisation du courant. Cette opération se fait facilement avec un tableur de type EXCEL.
Avec les données connues, le courant appelé en point fixe avec l’hélice choisie 18 X 7,5 est de I = 55,5 A ( Rappel du courant max spécifié par constructeur 60A)
Le Kv réel du moteur est alors évalue à 349,4
Avec une force électromotrice de 25,2 V ( batterie chargée) la tension Vm = E –R I est alors de 21,42 V
13 / 21 27/11/2020
La vitesse de rotation de l’hélice donnée par T/m = Kv Vm = 349,4 x 21,42 = 7485 T/m La puissance motrice disponible est Pm = Vm ( I- I° ) = 21,42 ( 55,5 - 1 ) = 1168 W Compte tenu de ces données, la traction en point fixe est
T = Ct d N^2 D^4 avec Ct = 0,083, N = 7485/60 =125 T/s , D =0,46m d = 1,2kg/m3
T = 68 N ou 6,9 kg ( traction au décollage ,batterie chargée)
12) Conséquences sur la distance et vitesse de décollage
Nous avons déjà calculé la vitesse minimum de vol aux environs de 10,3m/s
Comme la force de traction est de 68 N et en prenant une marge de 20% sur la vitesse de décollage, la distance nécessaire est donnée par
F =M γ
Donc γ = 68/6,9 = 9,8 m/s2
La vitesse de décollage estimée ici à 12 m/s est atteinte en t = 12/ 9,8 = 1,2 s
La distance parcourue est de D = 1⁄2 γ t2 = 7,3 m.
La distance décollage est de l’ordre de 7m à 8m
En fait pour être plus précis,il faut tenir compte du flux d’air envoyé par l’hélice sous les ailes. Ce flux va provoquer une portance supplémentaire et faciliter le décollage ( tant que le moteur tourne ) ;
Pour faire ce calcul on suppose
1) Le flux d’air de l’hélice concerne que la surface alaire comprise dans le cylindre défini par le plan de rotation de l’hélice, la surface occupée par le fuselage étant décompté.
2) La vitesse de ce flux d’air est donnée par le Pas de l’hélice x Vitesse de rotation 7,5x 2,52/100 x 125 = 23,6 m/s
3) Le Cz applicable au flux d’air de l’hélice est celui de la finesse max de vol Cz = 0,8
Avec ces données la surface portante intéressée par le flux d’hélice est (Diamètre de l’hélice – largeur du fuselage) x corde de l’aile soit
D x l = ( 0,46 – 0,14 ) x 0,29 = 0,093 m2
La portance supplémentaire apportée par ce flux est évaluée à P(+) = 1⁄2 d Cz S V2 = 0,5 x 1,2 x 0,8 x 0,093 x 23,62 = 25 N
Tout se passe alors comme si l’avion pesait 2,5 kg en moins. Ce flux va donc diminuer la vitesse minimum de décollage
14 / 21 27/11/2020
Le poids apparent est alors de 5,32 – 2,5 = 2,8 kg
En appliquant la formule V2 = 2 m g / ( d Cz S )avec une masse de 2,8 kg, la vitesse de décollage est de 7,5 m/s soit de 27 km/h.
Avec une marge voisine de 10%, la vitesse de décollage en tenant compte du flux d’hélice est de l’ordre de 30 km/h.
13) Performance en Vol de croisière
Le calcul réalisé aux paragraphes précédents donne une vitesse de croisière aux voisinages de la finesse maximum de 14 m/s ( 50 km/h)
Dans ces condition la traînée globale de l’avion est 0,61 N ou environ de 0,367 kg
Cette traînée doit être compensée par la traction de l’hélice, pour maintenir cette vitesse.
En fait la traction de l’hélice dépend du paramètre Ct, qui lui même dépend de J = V /(ND)
Les courbes donnant Ct en fonction de J va donc permettre de trouver le point de fonctionnement de l’hélice.
Les courbes du paragraphe 8 permettent d’approximer la fonction Ct par une droite en fonction de J
Pour ce qui concerne le coefficient Cp, il est possible d’approximer la fonction par une équation du 2° degrés.
Ainsi Ct = A J + B avec A = - 0,16667 et B = 0,1
De même
Cp = G J2 + H J + K avec G = -0,0833, H = 0,0083, K = 0,0250
13 -1)
On doit avoir
Point de fonctionnement en J de l’hélice pendant le vol de croisière
La traînée = La traction de l’hélice
1⁄2 d Cx S V2
Cx S V2 = 2 Ct N2 D^4
= Ct d N2 D^4
En faisant apparaître J = V / ( ND )
Cx S J2 = 2 Ct D2
En nommant le coefficient X = 2 D2 /( Cx S )
15 / 21
27/11/2020
J2 = X Ct en remplaçant Ct par sa fonction de J on a = X ( -0,16667 J + 0,1) J2 = X ( -0,16667 J + 0,1)
J2 + 0,1667 X J – 0,1 X J = 0
Le terme X = 2 D2 / ( Cx S ) est déterminé numériquement
X = 2 * 0,462 / ( 0,046 * 0 ,67 ) = 13,7
L’équation J2 + 0,1667 X J – 0,1 X J = 0 donne 2 solutions pour J
Une solution négative, qui correspondrait à une vitesse négative ( ou un fonctionnement en éolienne) et une solution positive qui correspond bien à une vitesse positive et en traction
Le point de fonctionnement en J de l’hélice est
J = 0,49
13-2) Vitesse hélice en vol de croisière
A ce niveau du calcul le diamètre de l’hélice est fixé ainsi que la vitesse de croisière calculée à 14 m/s.
La vitesse de rotation de l’hélice sera donnée par Donc N = V /( J D )
N = 14 / ( 0,46 *0,49)
N = 62 T/s
J = V ( ND )
T/m = 62 *60 = 3725 T/minutes
13-3) Puissance en vol de croisière
Connaissant le J de fonctionnement de l’hélice, il est possible de calculer le Cp et comme la vitesse de rotation est déterminée, la puissance à fournir à l’axe moteur.
La précision des courbes à ce niveau est médiocre, mais la meilleure estimation du Cp de l’hélice est
Cp = G J2 + H J + K avec G = G J2= 0,020
HJ = 0,00407
K = 0,0250
-0,0833,
H = 0,0083, K = 0,0250
16 / 21
27/11/2020
Cp = 0,0091
Avec un régime de rotation de 62 T/s, la puissance à fournir est P = Cp d N^3 D^5
P = 0,0091 * 1,2 * 62^3 * 0,46^5 = 56 W
Le moteur doit donc fournir 56 W en tournant à 62 T/s
13-4) Calcul du courant nécessaire en vol de croisière
Comme le moteur doit tourner à 62 T/s ou 3725 T/m cela implique que T/m=Kv Vmou N=KvVm/60
Vm = Tm /Kv
Laloid’OhmE=Vm–RI imposelecourantbatterieI= (E–Vm) /R Si on tient compte des variations de Kv avec le courant moteur
Kv = Kv° - W I
La tension Vm qu’il faut imposer au moteur est donnée par
Vm= Tm /(Kv°-WI)
Vm ( Kv° - WI ) = Tm
Vm [ Kv° - W(E – Vm) /R ] = Tm
En multipliant les 2 termes par R
Vm Kv° R – WE Vm + Vm2 = TmR
Ce qui s’écrit sous forme d’une équation du 2° degrés
W Vm2 + Vm ( Kv° R –WE ) – TmR = 0
Pour faire un calcul qui soit le plus réaliste possible on prendra comme force électromotrice de la batteries a tension à la charge 50 % soit 22,2 V
Donc ici E = 22,2 V
W à déjà était calculé W = 0,63 La résistance totale R = 68 mΩ
Tm= 62
17 / 21
27/11/2020
Le calcul donne 2 solutions
Vm = 12,8 V Vm = - 31,4 V
La solution 12,8 V est compatible avec la tension batterie de 22,2 V
Si la tension Vm est de 12,8V liée à la vitesse de rotation moteur, cela implique d’après la loi d’ohm lorsque le contrôleur conduit que le courant crête débité par la batterie atteint la valeur de
I = ( E – Vm ) R
I=(22,2–12,8)/0,068= 138,2A
La puissance demandée au moteur est de 56 W
Le courant moyen nécessaire au fonctionnement du moteur est donné par
Pour Pm=VmImpour Im=56/12,8= 4,37A
Il faut ajouter à ce courant le courant à vide estimé à 1A
Au total, le courant moyen est 4,37 + 1 = 5,37 A
C’est le contrôleur grâce à la modulation PWM qui « hachera » le courant crête de 138,2A pour obtenir le courant moyen de 5,37A nécessaire .
13-5) Réglage du PWM en vol de croisière
Ce courant moyen sera obtenu avec un PWM dont le rapport cyclique t /T 5,37 = 138,2 T /t et donc
T / t = 0,0388
14) Calcul de l’autonomie de vol
En considérant une batterie de propulsion 5 Ah et en admettant que pour des raisons de sécurité, on s’impose de décharger la batterie à 80%, la capacité disponible pour le vol est donc
5 *0,8 = 4 Ah utilisable avec une marge de 20 %
Avec une décharge aux environ de 5,4 A, la durée du vol est limitée à 4 /5,4 = 0,74 heure ou 44 minutes
L’autonomie de vol est de l’ordre de 3/4 heure avec une marge disponible de 20%
18 / 21 27/11/2020
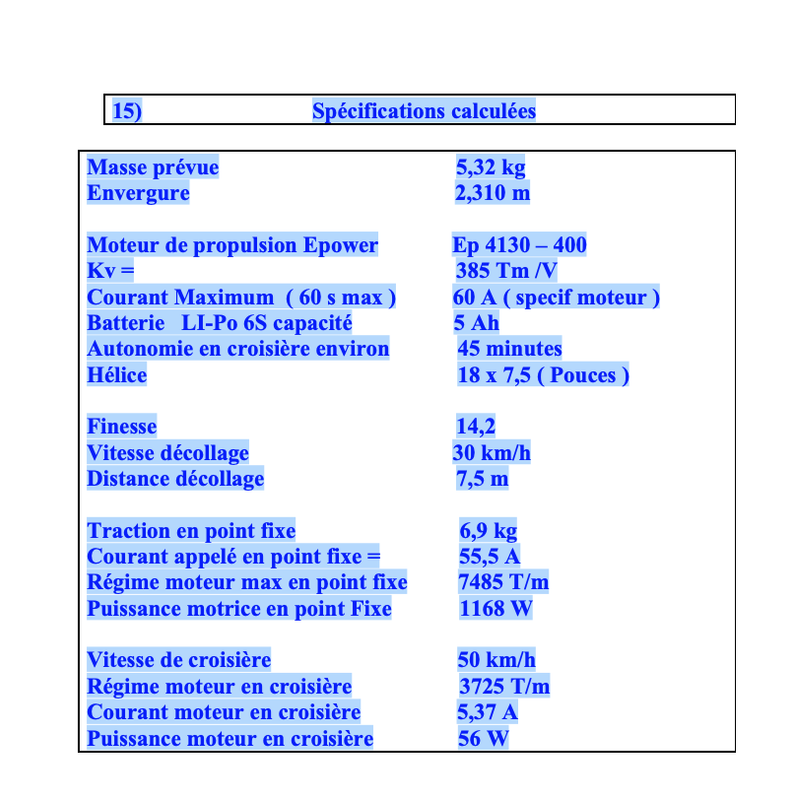
15)
Masse prévue Envergure
Moteur de propulsion Epower Kv =
Courant Maximum ( 60 s max ) Batterie LI-Po 6S capacité Autonomie en croisière environ Hélice
Finesse
Vitesse décollage Distance décollage
Traction en point fixe
Courant appelé en point fixe = Régime moteur max en point fixe Puissance motrice en point Fixe
Vitesse de croisière
Régime moteur en croisière Courant moteur en croisière Puissance moteur en croisière
Spécifications calculées
5,32 kg 2,310 m
Ep 4130 – 400 385 Tm /V
60 A ( specif moteur ) 5 Ah
45 minutes
18 x 7,5 ( Pouces )
14,2
30 km/h
7,5 m
6,9 kg 55,5 A 7485 T/m 1168 W
50 km/h 3725 T/m
5,37 A 56 W
19 / 21
27/11/2020
Ci-dessous Le Piper d’Olivier à l’échelle 2 du Piper d’Alain !!!!
20 / 21 27/11/2020
10 9 8 7 6 5 4 3 2 1
9 8 7 6 5 4 3 2 1
ANNEXE : Optimisation de l’hélice
Traction et Pas enfonction du diametre
Traction = poids
traction point fixe
PAS
00 12 13 14 15 16 17 18 19 20 Diametre helice
80
70
60
50
40
30
20
10
80
70
60
50
40
30
20
10
Limite specifiée moteur
Autonomie et Courant moteur
autonomie
courant moteur Point fixe
00 12 13 14 15 16 17 18 19 20 Diametre helice ( calage 10°)
21 / 21
27/11/2020
minutes Traction en kg -
 Merci beaucoup Daniel !
Merci beaucoup Daniel !
Je copie-colle toutes ces informations, et étudie ça attentivement.
Bons vols à toi
Jean-Philippe -
-
 Merci !
Merci !
Répondre à ce message
Vous n'êtes pas autorisé à poster un message sur le forum.